Stikprøve: En stikprøve er en delmængde af en population. For at en stikprøve kan anvendes til statistiske beregninger skal den være repræsentativ for den population man ønsker at undersøge, dvs. at hvis man udtog 100 tilfældige stikprøver fra samme population ville de ligne hinanden. Hvis stikprøven er tilpas stor, vil resultatet af en statistisk test med rimelig sandsynlighed være repræsentativt for resten af den population, hvorfra stikprøven har sin oprindelse. F.eks. kan I som klasse antages at være en stikprøve, som repræsentere danske gymnasieelever.
Middelværdi: En variabels middelværdien (μ) svarer til at finde gennemsnittet af alle tallene tilhørende variablen. Matematisk skrives det sådan:
Hvor x er den variabel, som man ønsker at undersøge og N er antallet af data punkter. Dvs. summen af alle datapunkter divideret med antallet.
Median: Medianen er den værdi, som svarer til den indeksmæssige midterste værdi, hvis man sorterede data. Dvs. hvis man stillede alle tallene i en variabel op i den numeriske korrekte rækkefølge (lavest værdi til højeste værdi), vil medianen svare til den midterste værdi i rækken.
Varians: Varians er et begreb, som angiver hvor store udsving, der er i værdierne af en stokastisk variabel. Varians er altså et mål for, hvor meget den stokastiske variabels værdier i gennemsnit afviger fra middelværdien. Variansen skrives matematisk således
Hvor xn er hvert datapunkt i variablen, μ er middelværdien og N er antallet af observationer.
Standardafvigelse: Kaldes også spredning (σ ) er ligesom variansen et mål for, hvor meget en tilfældig variabel i et datasæt afviger fra middelværdien af datasættet. Hvis standardafvigelsen er stor, betyder det at data i gennemsnit ligger langt fra middelværdien. Standardafvigelsen er blot kvadratroden af variansen:
Fordelen ved at bruge standardafvigelse frem for varians, er at standardafvigelsen har samme enhed som data, hvilket gør det lettere at tolke på resultatet.
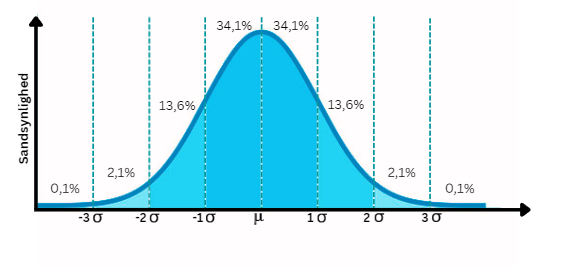
Fordeling: En fordeling beskriver, hvordan værdierne i en observeret stikprøve fordeler sig i forhold til middelværdien. Mange stokastiske variabler vil være normal fordelte, dvs. at de fleste værdier vil ligge tæt op ad middelværdien, mens antallet af observationer som repræsenterer en bestemt værdi vil falde, jo længere væk den bevæger sig fra middelværdien. Fordelingen vil tilmed være ensartet på begge sider af middelværdien og danne en klokkeformet kurve. Bredden af klokkeformen afhænger af standardafvigelsen. For en normalfordeling gælder det at ±1σ svare til de midterste 68,2 % af arealet under kurven, som vist på figur 1. Der findes andre former for fordelinger, disse vil vi dog se bort fra i dette kompendium. For simplificeringen antager vi at det data, vi arbejder med, er normalt fordelt.
P-værdier: En p-værdi er sandsynligheden (altså et tal fra 0-1) for at opnå et testresultat, der er mindst lige så ekstrem som de data man har observeret, under en bestemt hypotese, f.eks. at to grupper er ens. Hvis p-værdien er høj, vil det betyde at den/de observationer man tester, stemmer overens med ens hypotese. Hvis den derimod er meget lille (typisk <0.05) antager man at der er en signifikant forskel mellem ens hypotese og de observerede data. I dette tilfælde vil man forkaste sin hypotese, som typisk kunne være at de to grupper er ens. Hvordan p-værdien beregnes, afhænger af hvilken statistisk test man anvender.
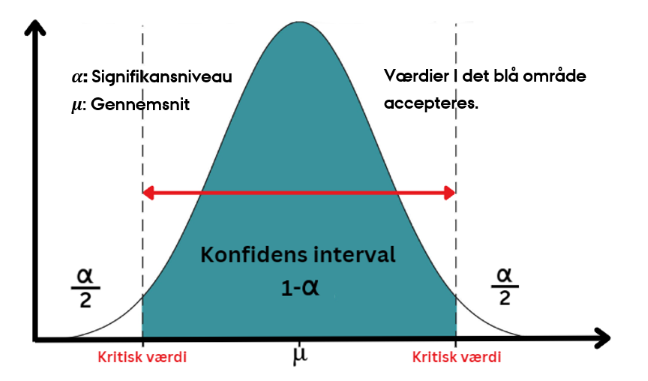
Konfidensintervaller: Et interval, der ligger rundt om middelværdien, hvor man antager at observationer indenfor dette interval tilhører populationen. Et typisk anvendt konfidensinterval er 95%, d.v.s. at observationer der ligger udenfor konfidensintervallet kun med en lille sandsynlighed stammer fra populationsfordelingen. Et konfidensinterval på 95 % kan beregnes ud fra middelværdien (μ ) og standardafvigelsen (σ) , men den præcises udregning afhænger af hvordan fordelingen af data ser ud. Hvis data er normalfordelt, vil et konfidensinterval (KI) på 95 % kunne beregnes med følgende matematiske formel:
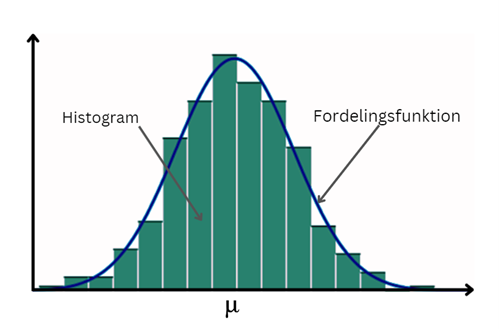
Histogram: Fordelingen af data er typisk illustreret ved et histogram. Et histogram er en grafisk fremstilling af data, hvor man grupperer data i intervaller og for hvert interval tæller hvor mange observationer der falder indenfor dette interval. Hen ad x-aksen vil intervallerne være angivet, mens y-aksen viser, hvor mange datapunkter som tilhører hvert enkelt interval.
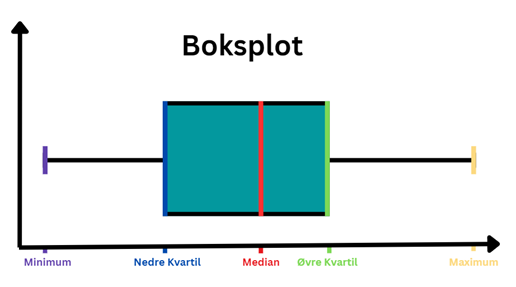
Boksplot: Et boksplot er også en grafisk måde at illustrere data på. For at lave et boksplot beregnes først kvartilerne. Ved kvartilerne opdeles det sorterede data i de 25 % laveste, 25 % næste lavest, 25 % næst højeste og de 25 % højeste værdier. Et boksplot afspejler de fire kvartiler og kan derved også være en brugbar måde at illustrere fordelingen af data på.
I forrige afsnit blev nogle grundlæggende begreber for statistik gennemgået. I dette afsnit vil du blive introduceret til, hvordan man kan teste for forskelle mellem to populationer af data. En meget afvendt gruppe af statistiske test er hypotesetests. Begrebet hypotesetest dækker over statistiske metoder til at undersøge, hvorvidt en hypotese er understøttet af observeret data. Man tester altså om en hypotese, som f.eks. udtaler sig om bestemte egenskaber ved en population, kan accepteres eller bør forkastes, ud fra sandsynlighederne for at de passer på de observerede data. Det kan f.eks. være at man antager at middelværdien af søvnmængde hos mænd og kvinder i Danmark er ens. I dette tilfælde vil man lave to stikprøver som er repræsentative for hhv. danske mænd og kvinder, og teste hvorvidt hypotesen kan accepteres ud fra de observerede stikprøver.
Der findes forskellige former for hypotesetest, men den generelle fremgangsmåde består af følgende 6 trin:
Dvs. at middelværdien for de to populationer er ens. Den alternative hypotese til denne test er derfor:
Dvs. at middelværdien for de to populationer ikke er ens.
Der findes talrige computerprogrammer, som kan anvendes til at beregne test-størrelser og p-værdier af alt fra små til meget store datasæt, det er derfor ikke absolut nødvendigt at have den fulde forståelse for de underliggende matematiske beregninger. Det er dog essentielt at kunne anvende den rigtige fremgangsmetode samt forholde sig til resultatet, for at kunne få gavn af regneprogrammerne. I de følgende to underafsnit, vil to typer af hypotese test blive præsenteret. Formålet er at kunne forstå testene i en sådan grad at I bliver i stand til udføre dem på data vha. et regneprogram samt kunne redegøre for og konkludere på resultatet.
En af de mest anvendte hypotesetest er gruppen af t-tests. En t-test bruges til at teste for forskelle i middelværdier mellem stikprøver. Ved en t-test antager man at data er normalfordel omkring middelværdien. Dette kaldes også for en t-fordeling. T-testen er en effektiv metode til at teste for forskellen i middelværdien af to forskellige scenarier/grupper, f.eks. reaktionstiden hos personer som har sovet normalt mod personer, som ikke har sovet i 24 timer. Dog kræver t-testen at man på forhånd ved noget om fordelingen af data samt at fordelingen hos de to grupper er nogenlunde tilsvarende og normalfordelt. Dvs. at forskellen i standardafvigelsen mellem de to grupper ikke er for stor. Om dette er gældende, er dog ikke altid nemt at gennemskue ved små stikprøve størrelser.
T-test kan både laves som t-test med en stikprøve eller t-test med to stikprøver. Ved en t-test med en stikprøve testes stikprøven mod en forud bestemt middelværdi. Ved en t-test med to stikprøver, testes middelværdien for de to stikprøver mod hinanden. Man kan opdele t-test med to stikprøver, i parrede og uparrede. En parret t-test bruges for at teste to grupper af data, som på den ene eller anden måde er forbundet. Dette kunne f.eks. være to målinger fra samme person før og efter søvn. De uparret t-test bruges, som navnet antyder, til sammenligning af uparrede data f.eks. forskellen i søvnmængde hos børn vs. voksne. Det er vigtigt at kunne forholde sig til om data er parret eller ej, for at opnå et troværdigt testresultat.
T-test kan desuden være henholdsvis ensidet eller tosidet. Den ensidet t-test forkaster kun H0 , hvis μ2 er signifikant større (højreside) eller signifikant lavere (venstreside), mens den tosidet tester for begge ender i samme test. Ved den ensidet udgør signifikansniveauet på 5 % kun den ene side, mens den tosidet deler signifikansniveauet op og så hver side udgør 2.5 %.
En anden hypotese testmetode er permutationstest. Denne metode er særligt god til at teste små stikprøver og har den fordel, at den ikke kræver forud antagelser om fordelingen af data. Permutationstesten bygger nemlig selv en stikprøve fordeling ved gentagende gange at blandede to oprindelige stikprøver og udtrække nye tilfældige stikprøver fra den blandede pulje af data. Lad os prøve at forstå principperne bag en permutation test ved at tage et eksempel:
Antag at størrelsen af søvntimer det seneste døgn for en gruppe med nattevagt (gruppe 1) og en gruppe med normale arbejdstider (gruppe 2), er som angivet i tabellen under:
Gruppe 1 | Gruppe 2 |
7 | 8 |
6 | 9 |
6 | 8 |
5 | 8 |
5 | 7 |
6 | 8 |
7 | 7 |
Herefter ville der tilfældigt udtrækkes 7 værdier fra variablen G, som nu udgør en ny ”teoretisk stikprøve” for gruppe 1, som kaldes for x1:
Med middelværdien:
De tilbageværende data fra G udgør så den nye ”teoretiske” stikprøve for gruppe 2, som kaldes for y1:
Med middelværdien:
Differencen (f) mellem de to middelværdier bestemmes:
Dette gøres adskillige gange således at der dannes mange teoretiske differencer:
Hvor i er antallet af ”permutationer” (dvs. antal gange den ovenstående proces gentages). Herefter laves en fordeling over alle de teoretiske differenser. Denne fordeling afspejler altså, hvorledes de observerede stikprøverne kunne have set ud, hvis de var taget fra den samme population. Fra denne fordeling beregnes så et konfidensinterval og det testes herefter om forskellen i middelværdien mellem de to oprindelige grupper ligger inden for det beregnede konfidensinterval, hvis ikke forkastes hypotesen om at de to grupper der ens.